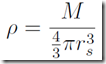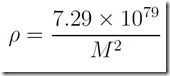A Black Hole Made of Water?

So while reading through twitter the other day I noticed a few folks posting that if you took the mass of a Black Hole and spread it out through its entire volume you would find that the density of this smeared-out black hole would have the same density of water.  This tripped my astronomer-senses right away.  A 1 solar mass black hole (that is a black hole with the same mass as our sun) has a classical, non-rotating radius of about 3 kilometers.  A 3 km ball of water won’t spontaneously collapse into a black hole, as evident by the the fact that our oceans and Jupiter’s moon Europa are not black holes right now.  While this statement was wrong, it got me thinking – “Could a Black Hole be massive enough for it to be true?”

In a classical sense this problem isn’t too tough to work out, I just need to find how the volume of a black hole scales with its mass and figure out where that gives a gross density of about 1000 kg/m³, the density of water (1 g/cm³ for those using cgs units!).

To make things easy on myself I’m taking a classic, non-rotating black hole, and assuming that the radius in question is the Event Horizon, where the local escape velocity equals the speed of light.   Take the equation of escape velocity v_e:

 

with G being Newton’s Gravitational Constant (6.67×10⁻¹¹ m³ kg⁻¹ s⁻²), M being the mass of the world one is trying to escape, and r the radius of that place.

Setting v_e equal to the speed of light c (3×10⁵ km/s) and solve for r one finds the radius for which the mass is enough to keep even light from escaping.  This is the Schwarzschild Radius.

 

Now this is a pretty small radius for most masses - as it should be since we don’t see ordinary things collapsing into black holes all around us!  A Black Hole with the mass of the Sun ends up with a radius of about 3 km.  An Earth-mass black hole would be about the size of a single playing die, and a person-mass Black Hole would be much smaller than a proton!

Now I can use that equation to find the radius of a Black Hole of a given mass.  To find the gross density rho I need to divide the Mass M by the volume of a sphere of radius r_s. 

Plugging in the Schwarzschild Radius we get

And finally using the the numerical values for all these constants we get the fairly simple

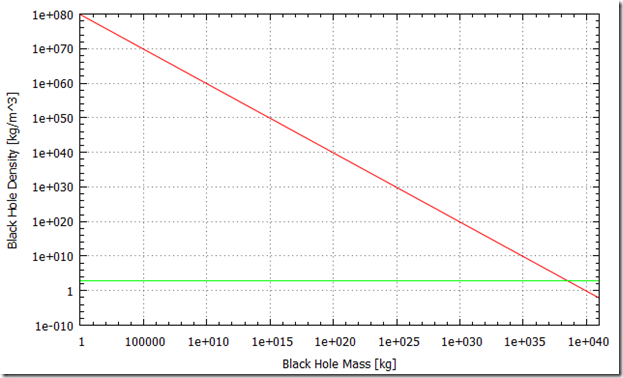
So the gross density enclosed within the event horizon of a black hole scales as 1/M².  Solving for the density of water (1000 kg/m³) I find that a black hole with a mass of about 2.7 x 10³⁸ kg would do it at a radius of about 4 x 10¹¹ km.  This is over the mass of 100 million Suns in a sphere about 90 times larger than the orbit of Neptune.  Huge, but there are Super Massive Black Holes that dwell at the center of galaxies that can achieve this mass.  While own Milky Way Galaxy has a central black hole with the mass of about 4.5 million Suns, too small for the water-density hypothesis, the most massive Galactic Black holes that we have detected check in at thousands of millions of solar masses!  These monsters (under this simple analysis) would indeed have a gross density that would be much less than water.  To visualize this I made up a quick and dirty plot showing Black Hole density on the y-axis and the Black Hole mass on the x-axis.  My simple density equation is the diagonal red line, while the strait line shows the density of water for comparison.  They cross right at a Black Hole mass of 2.7 x 10³⁸ kg. 

So while my astronomer-sense did kick in to point out that the statement about the gross density of a Black Hole being about the same as water is incorrect in general, there are known Black Holes that are massive enough for this to be true!  While the Black Holes left over after the death of a super-massive star or the Black Holes in the center of the Milky Way and Andromeda galaxies are far more dense than water, the super massive Black Holes found at the heart of giant elliptical galaxies, for example NGC 4889 located in the Coma Cluster end up being much less dense than water.